
Algorytmy i struktury danych. Szczegółowe omówienie
Witam wszystkich! Nazywam się Adam Leos. Obejmuję stanowisko Senior Software Engineer (ex Roku and Uber). Oprócz pracy podstawowej, biorę aktywny udział w rozwoju branży IT i wspomagam podnoszenie kwalifikacji zawodowych developerów. Na przykład, biorę udział w hackathonach (jako uczestnik i jako juror?), jestem autorem artykułów technicznych, prowadzę webinary i występuję z wykładami jako zaproszony specjalista techniczny w firmach i jako speaker na konferencjach.
Tematy swoich prezentacji wybieram w ten sposób, żeby to nie wyglądało jako promowanie siebie / firmy / technologii, a żeby ten materiał był pomocny i przydał się developerowi (najlepiej natychmiast). Jednym z takich tematów jest konieczność znajomości algorytmów i struktur danych. Z różnych powodów niektórzy deweloperzy z krajów WNP są przekonani, że taka wiedza nie jest potrzebna i nie jest ważna. Spoiler! Mylą się.
Dla kogo jest ten artykuł? Przyda się każdemu, kto chce osiągnąć jeden (lub kilka, można wszystkie) z poniższych celów:
- stwarzać produkty wysokiej jakości (wydajne i niezawodne);
- zarabiać dużo więcej niż średnie wynagrodzenie na rynku;
- unikać błędów na rozmowie kwalifikacyjnej i najlepiej zaprezentować siebie i swoje umiejętności zawodowe, starając się o pracę w najlepszych firmach na świecie;
- po prostu rozgryźć te algorytmy, ale w sposób bardzo prosty, dostępny i zrozumiały.
I nie ma żadnego znaczenia, jaki masz poziom kwalifikacji zawodowych developera i jaki kierunek wybrałeś. Materiał będzie pomocny zarówno dla początkujących developerów, jak i dla doświadczonych liderów technicznych.
Artykuł będzie oparty na dwóch tezach (oraz będzie obalać poniższe tezy):
- Pierwsza: „Znajomość struktur danych i algorytmów nie jest wymagana. Developer nie czerpie żadnych korzyści z tej wiedzy”. Zrozumiemy, dlaczego powyższe twierdzenie nie jest zgodne z prawdą i przeanalizujemy przykłady wzięte z życia, ponieważ stosowałem wiedzę w kilku firmach i osiągnąłem duży wzrost wydajności.
- Druga, którą słyszę od developerów, którzy są bardziej zaawansowani i uważają, że: „W sumie możemy czerpać korzyści z tej wiedzy, ale żeby zdobyć wiedzę, trzeba poświęcić wystarczająco dużo czasu na dokładne przestudiowanie materiału. A poza tym ten materiał jest bardzo trudny do ogarnięcia”. Zatem na początku artykułu przyswoimy wiedzę podstawową i skupimy się na opanowaniu materiału (porozmawiamy o złożoności algorytmu, notacji dużego O, sortowaniach, najbardziej popularnych strukturach i stosowaniu tych struktur do optymalizacji projektu).
Złożoność algorytmów
Aby ustalić wydajność / niewydajność jakiegokolwiek kodu i zrozumieć, co i w jaki sposób możemy zoptymalizować, powinniśmy wprowadzić jedno określenie i zawsze posługiwać się nim w artykule. Chodzi o złożoność algorytmu, czyli zależności ilości potrzebnych zasobów od rozmiaru danych wejściowych algorytmu. Następnie przeanalizujemy tę definicję z różnych punktów widzenia i podamy kilka przykładów.
Od razu chciałbym zwrócić Twoją uwagę na „zasoby”. Jakimi zasobami posługujemy się? Oczywiście czasem (czyli czas wykonania algorytmu: im dłużej wykonujemy tym więcej czasu poświęcamy © Cap). Ale, ku możliwemu zaskoczeniu wielu developerów, często posługujemy się jeszcze jednym zasobem (zarówno w front-end), chodzi o pamięć. Oczywiście pracując na nowiutkim MacBook Pro i korzystając z ostatniej wersji Chrome być może nigdy nie będziesz mierzył się z problemami z dostępnością pamięci (choć miałem podobne sytuacje, bo developerzy potrafią), ale pamięć jest tak samo cennym zasobem, jak i czas. Najdotkliwiej odczułem to pracując w kilku ostatnich firmach, zajmując się wytworzeniem oprogramowania dla różnych platform typu Smart TV, konsoli gier wideo ect., ponieważ sprzęt nie spełnia minimalnych wymagań (pod względem technicznym telewizor za $20 000 będzie gorszy od Twojego smartfonu, a co dopiero mówić o tańszych modelach).
A teraz spójrzmy na syntetyczny przykład (zaczniemy od rzeczy prostych i stopniowo będziemy mogli utrudniać, jednocześnie przechodząc od syntetycznych przykładów do przykładów z życia codziennego). Na tym przykładzie będziemy obliczać sumę wszystkich liczb zawartych w tablicach.
function sumNumbersInArray(array) {
let sum = 0;
array.forEach(number => sum += number);
return sum;
}
Tu otrzymaliśmy zbiór, podaliśmy zmienną, początkowo równą 0, i uruchamiamy iterację tablicy, wybierając każdy element zbioru i dodając go do sumy. Wszystko jest proste. Przeanalizujmy teraz: co się stanie, jeśli wywołamy funkcję, obejmującą zbiór, składający się z 5 elementów [1, 2, 3, 4, 5]? Oczywiście wykonamy 5 iteracji — dla każdego elementu w tablicy, aby dodać go do sumy. A co wtedy, jeśli tablica będzie się składać z dziesięciu elementów? Logika podpowiada, że trzeba będzie wykonać dziesięć iteracji.
To jest oczywiste: im większa tablica, tym więcej iteracji wykonujemy (odpowiednio więcej czasu tracimy na realizację). Wyżej określiliśmy złożoność algorytmu i, pamiętając o powyższych założeniach (wzrost zużycia zasobów w zależności od wzrostu rozmiaru danych wejściowych), zobaczymy jak wzrastało zużycie zasobów w naszym przypadku (nakłady czasu – więcej iteracji) w zależności od wzrostu rozmiaru danych wejściowych (tablica – input). Tak więc w przypadku naszego algorytmu mamy do czynienia z zależnością liniową od danych wejściowych: każdy element zbioru wymaga dodatkowej iteracji.
Notacja dużego O
Najlepiej przedstawiają zależności wykresy, i do opisu takich zależności służy notacja dużego O (chodzi o O(n), O(log n) i inne, które przeanalizujemy dalej). Gdyby trzeba to było opisać jednym zdaniem, to by brzmiało następująco: funkcja opisująca wzrost złożoności algorytmu. Co to takiego złożoność algorytmu i jak ona może wzrastać – mniej-więcej mamy pojęcie. Duże O – jest to funkcja, która opisuje ten wzrost. Chciałbym tylko doprecyzować: funkcja tutaj występuje w sensie matematycznym, czyli jako funkcja, służąca do tworzenia wykresu.
Weźmiemy nasz kod syntetyczny z przykładu wyżej i stworzymy wykres przedstawiający zależności wielkości danych wejściowych od liczby iteracji. Na osi X (poziomej) niech będzie wzrost danych wejściowych od 0 do jakiejś liczby skończonej n. Niech głównymi punktami będą 1, 100, 1000 i 10 000 (elementów w tablicach). Na osi Y (pionowej) będzie pokazany wzrost liczby operacji także od 0 wzwyż z punktami głównymi 1, 100, 1000, 10 000 operacji. Pozostaje nam tylko narysowanie linii zależności, którą mieliśmy w algorytmie.
Jak pamiętacie, dla każdego elementu w tablicy musimy wykonać dodatkową operację dodawania. To oznacza, że jeżeli uzyskujemy 100 elementów, wykonujemy 100 operacji. Uzyskujemy 10 000 elementów, wykonujemy 10 000 operacji. Uzyskujemy n elementów, wykonujemy n operacji. I to jest właśnie ta sama n w O(n), która nazywana jest także złożonością liniową. Wszystko jest bardzo proste.
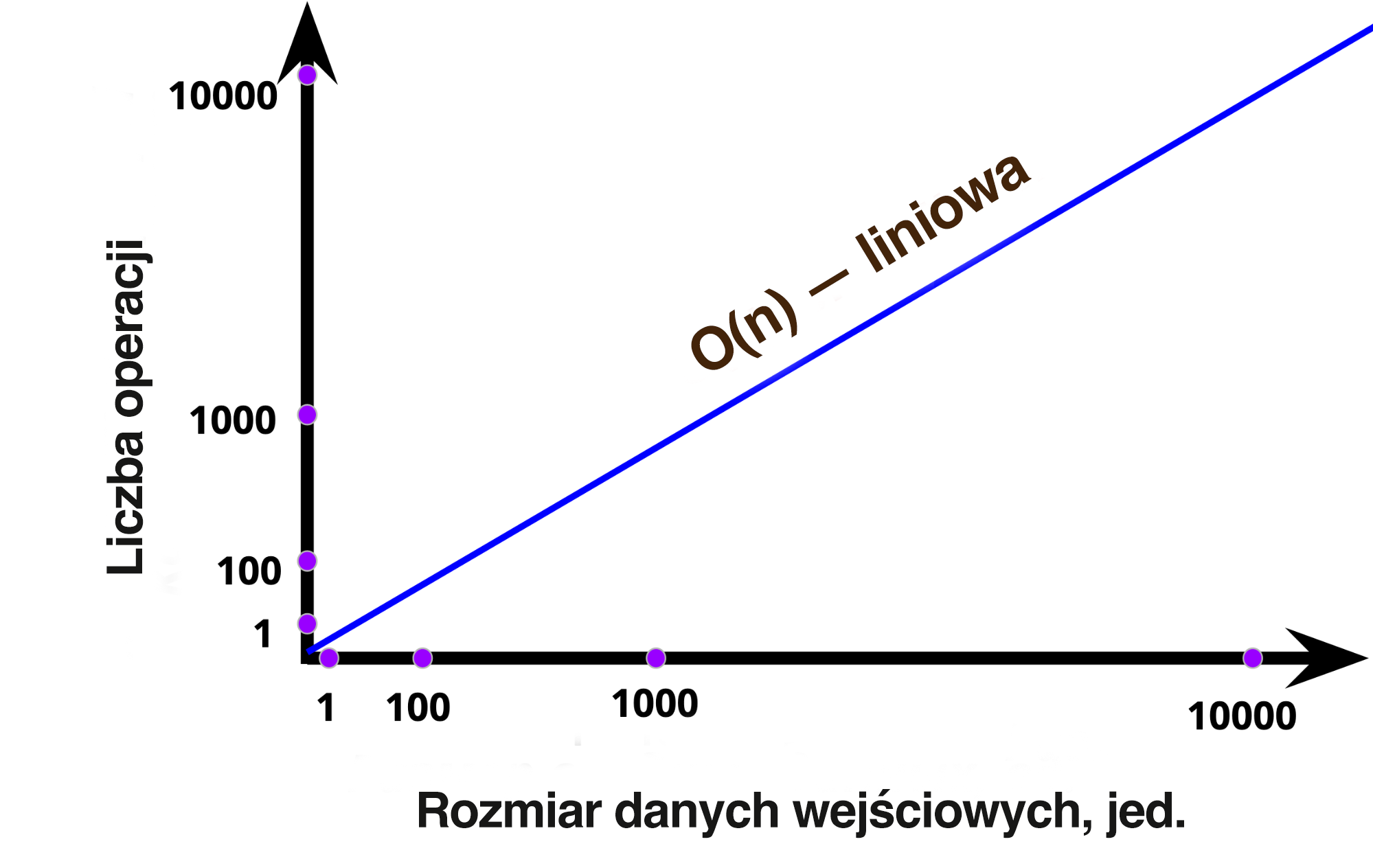
Tutaj wszystko jest fajnie, tyko powinniśmy spojrzeć na to pod różnymi kątami i podać inne przykłady, żeby utrwalić w pamięci przeczytany materiał. Przeanalizujemy nowy przykład prostyObliczyć (simpleCalculate). Nic nie przyjmujemy i wykonujemy jakieś tam operacje: obliczamy zmienne, wypisujemy coś do konsoli (żeby mieć więcej operacji) i zwracamy różnicę.
function simpleCalculate() {
const a = 1 + 2;
const b = 3 + 4;
console.log('calculating...');
return b — a;
}
Złożoność takiego algorytmu O(1) jest stała. Tutaj także wszystko jest prymitywne: nasz algorytm w ogóle niczego nie przyjmuje, więc nie jest w żaden sposób uzależniony od danych wejściowych. Zatem gdybyśmy nawet z jakiegokolwiek powodu wprowadzali różnego rodzaju wartości, algorytm cały czas wykonywałby te same operacje, pod żadnym pozorem nie zmieniając ilości wykorzystywanych zasobów, dlatego nazywamy to złożonością stałą. Na wykresie jest to zaprezentowane w jeszcze bardziej przystępny sposób:
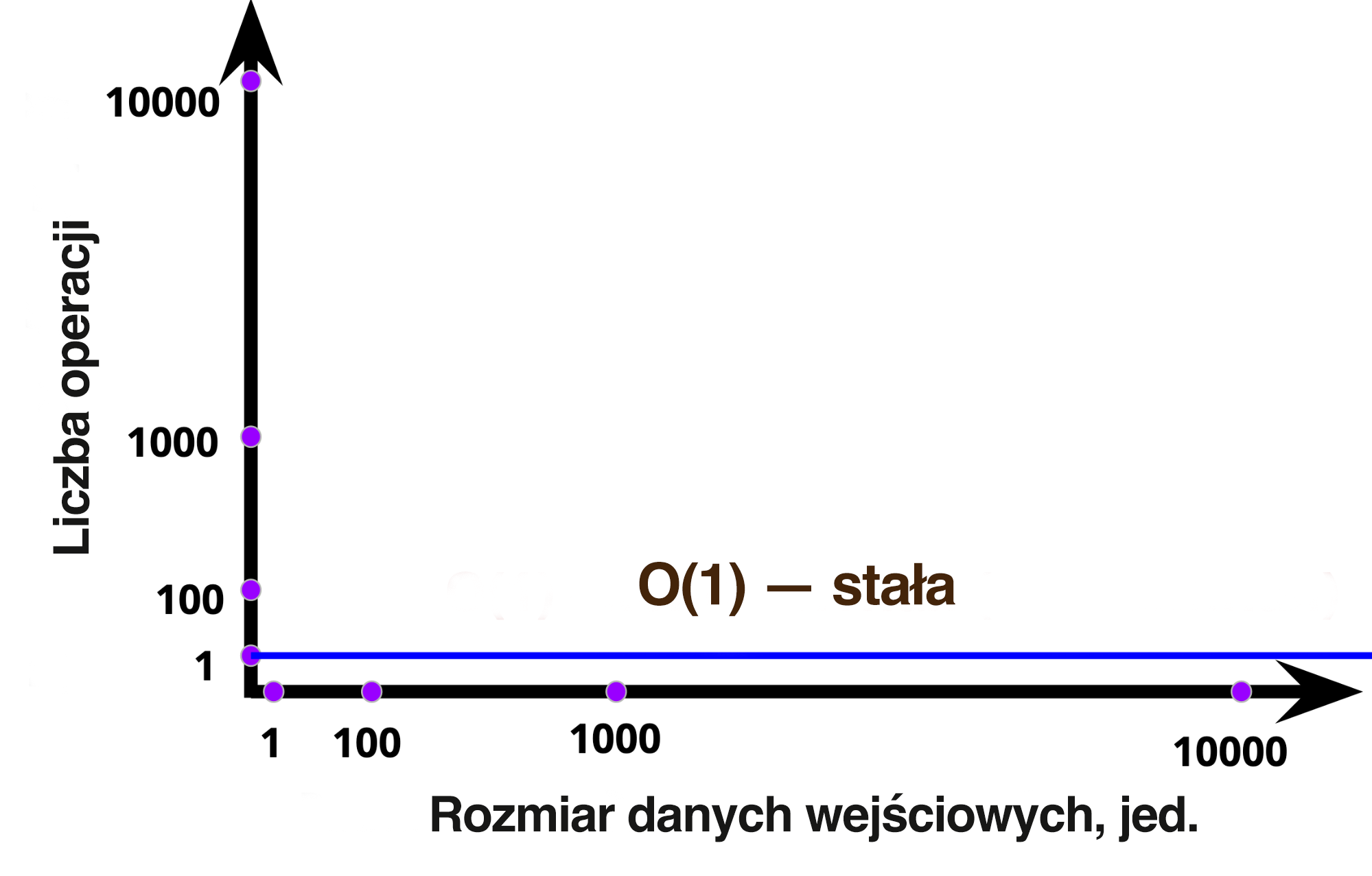
Jak wynika z wykresu, mamy tylko prostą linię: algorytm wykonuje się w stałej ilości operacji, niezależnie od liczby danych wejściowych. Natomiast trzeba tu zrozumieć jedną ważną rzecz – chodzi o oznaczenie złożoności O(1). Jedynka nie wskazuje na liczbę operacji i nie będzie się zmieniać, jeżeli algorytm będzie wykonywał większą liczbę operacji (przynajmniej nasz algorytm również wykonuje większą liczbę operacji). Tutaj jedynka, tak samo jak n w O(n), jest znakiem specjalnym, czyli w tym przypadku jedynie symbolem złożoności stałej.
A co się stanie, jeżeli będziemy przyjmować liczbę jako argument funkcji i dodawać ją do naszej różnicy? Jaka będzie złożoność kolejnego kodu?
function simpleCalculate(number) {
const a = 1 + 2;
const b = 3 + 4;
console.log('calculating...');
return b — a + number;
}
Złożoność tego algorytmu tak samo będzie O(1). Mimo, że już przyjmujemy argument i stosujemy go, nasze czynności polegają jedynie na jednej dodatkowej operacji dodawania. Bez względu na to, jaka to liczba – duża, mała, ułamkowa czy ujemna – zawsze po prostu bierzemy ją i dodajemy w wyniku jednej operacji (oczywiście, pod warunkiem, że to się zmieści w pamięci, ale to już zupełnie inna historia), czyli liczba operacji jest stała i nie zależy od inputu.
No dobrze, a kiedy w takim razie powstaje zależność? Najprościej będzie po prostu pokazać to używając tablicy, gdybyśmy przyjmowali tablice i na końcu obliczyli dodatkową liczbę do dodania, iterując po tablicy.
function simpleCalculate(array) {
const a = 1 + 2;
const b = 3 + 4;
let additionalNumber = 0;
array.forEach(num => additionalNumber += num);
return b — a + additionalNumber;
}
Tu u nas znów pojawia się zależność liniowa od danych wejściowych, z którą mieliśmy do czynienia, kiedy omawialiśmy pierwszy przykład. Im większe są tablice, tym więcej operacji wykonujemy w celu obliczenia składnika dodatkowego. Pamiętacie złożoność takiego algorytmu? O(n).
Świetnie, teraz wielu z was może się wydać, że rozgryźliście system: jeżeli dane wejściowe zawsze stanowią zbiór, to złożoność zawsze będzie liniowa, О(n), i nie ma się nad czym zastanawiać. Ale możemy spojrzeć na taką wersję poprzedniego kodu.
function simpleCalculate(array) {
const a = 1 + 2;
const b = 3 + 4;
const additionalNumber = array.length;
return b — a + additionalNumber;
}
Tym razem, wciąż przyjmując tablicę argumentów, po prostu bierzemy jej długość jako dodatkową liczbę do dodawania. A określanie rozmiaru tablicy, przechowywanego osobnie, stanowi natychmiastową (stałą) operację. Dlatego bez względu na to, jaką tablicę tutaj zweryfikowaliśmy, zawsze będziemy natychmiast określać jej długość i za pomocą jednej operacji dodawać do różnicy. Zatem jest to złożoność stała, O(1).
Dalej przytoczymy kolejny przykład. Powiedzmy, że mamy tablice, i chcemy dodać wszystkie elementy do wszystkich – po to będziemy posługiwać się zagnieżdżoną podwójną pętlą.
function notSoSimpleCalculate(array) {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
array[i] = array[i] + array[j];
}
}
return array;
}
Złożoność takiego algorytmu jest już znacznie większa, dla każdego elementu tablicy musimy wykonać pełną iterację po tablicy. Czyli, posługując się tylko tablicą składającą się z pięciu elementów [1, 2, 3, 4, 5], wykonujemy 25 operacji. Stosując prostą matematykę, możemy dojść do wniosku, że biorąc pod uwagę wielkość naszych danych wejściowych będzie potrzebny kwadrat operacji. Taka złożoność nazywa się kwadratową i jest oznaczana О(n^2). Wykres pokazuje gwałtownie rosnące wykorzystanie zasobów takiego algorytmu.
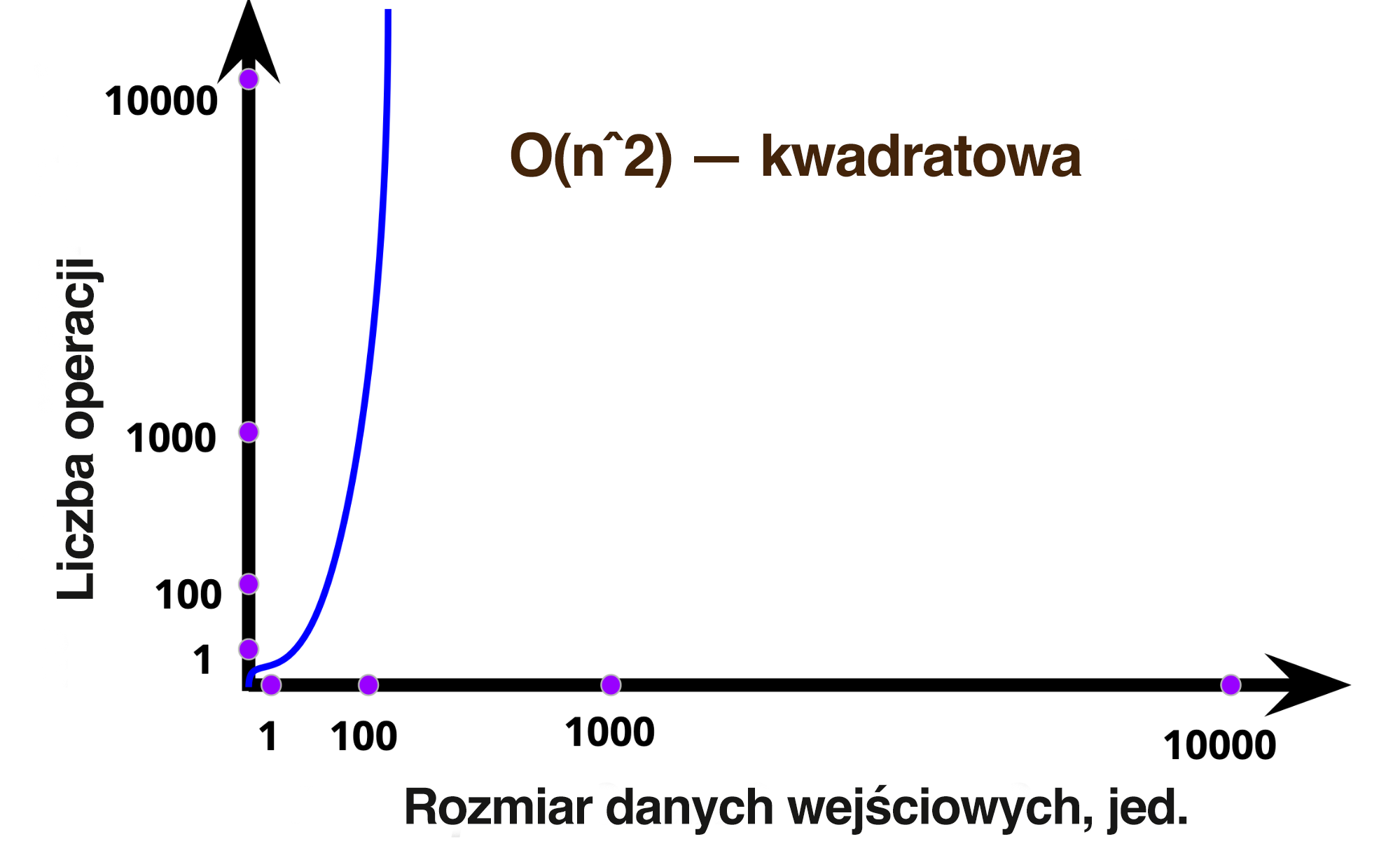
I jeśli jest to oczywiste w przypadku zagnieżdżonej pętli, to tutaj na developera może czekać nieoczekiwany gwałtowny wzrost złożoności.
function mightBeSimpleCalculate(array) {
let total = 0;
array.forEach(num => {
const additional = array.indexOf(num) > 5 ? 5 : 1;
total = total + num + additional;
});
return array;
}
Jak można się domyślić, złożoność takiego algorytmu wynosi O(n^2). Właściwie występuje tutaj ta sama zagnieżdżona pętla. Stosowanie metody indexOf – jest to zwykła pętla, weryfikacja tabeli: ponieważ indeksy każdego elementu nie są przechowywane w tablicy, trzeba go znaleźć. Oczywiście doświadczony developer wie o tym. Co prawda, jeżeli doświadczony programista nie zna algorytmów, najprawdopodobniej nie będzie zmieniał tego kodu. Swoją drogą, optymalizacja w takim przypadku byłaby mega prosta. Drugi argument w metodzie forEach – indeks elementu iterowalnego, i bez najmniejszego problemu złożoność kwadratowa zamienia się w liniową, potencjalnie oszczędzając dużą ilość zasobów niezbędnych do wykonania.
function mightBeSimpleCalculate(array) {
let total = 0;
array.forEach((num, index) => {
const additional = index > 5 ? 5 : 1;
total = total + num + additional;
});
return array;
}Ostatnim ważnym punktem w tym rozdziale będzie wzmianka, że notacja dużego O wskazuje na szybkie tempo wzrostu złożoności algorytmu i ignoruje optymalizacje stałe. Uzupełnijmy nasz przykład zagnieżdżonych pętli o kolejną pętlę liniową:
function notSoSimpleCalculate(array) {
// dodatkowo, wyświetlamy każdy element w konsoli
array.forEach(num => console.log(num));
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
array[i] = array[i] + array[j];
}
}
return array;
}Złożoność tego algorytmu będzie nie O(n + n^2), a po prostu kwadratowa, O(n^2), właśnie dlatego, że kwadrat będzie rósł niewspółmiernie szybko, przez co wpływ złożoności liniowej będzie nieistotny.
Przykład wzrostu w liczbach
Żeby zobaczyć różnicę, warto spojrzeć na liczbę operacji w zależności od złożoności o jednakowych wielkościach danych wejściowych. Przeanalizujemy sytuację, polegającą na tym, że weryfikujemy tablice zawierające 10 000 (dziesięć tysięcy) elementów, i ustalimy, ile operacji wykonamy w przypadku różnego rodzaju złożoności:
- O(1), złożoność stała – 1 (jedna) operacja;
- O(log n), złożoność logarytmiczna (np. wyszukiwanie binarne) — ~13 (trochę ponad trzynaście) operacji;
- О(n), złożoność liniowa – 10 000 (dziesięć tysięcy) operacji;
- О(n^2), złożoność kwadratowa – 100 000 000 (sto milionów) operacji;
- O(n^3), złożoność sześcienna (gdybyśmy mieli do czynienia z zagnieżdżoną potrójną pętlą) – 1 000 000 000 000 (jeden bilion) operacji;
- O(n!), złożoność „rzędu n-silnia” (wyszukiwanie wszystkich zmian, np. rozwiązanie przykładowego problemu komiwojażera) — 10 000 000 000 000 000 000 000 000... i jeszcze mnóstwo zer. Aby sobie lepiej uzmysłowić czas wykonania: Za biliony lat umrze Wszechświat i dopiero po tym wykonywanie algorytmu się zakończy.
Jest też dobry obrazek, na którym wykresy przedstawiające różne rodzaje złożoności sąsiadują ze sobą. Ten obrazek unaoczniają różnice:
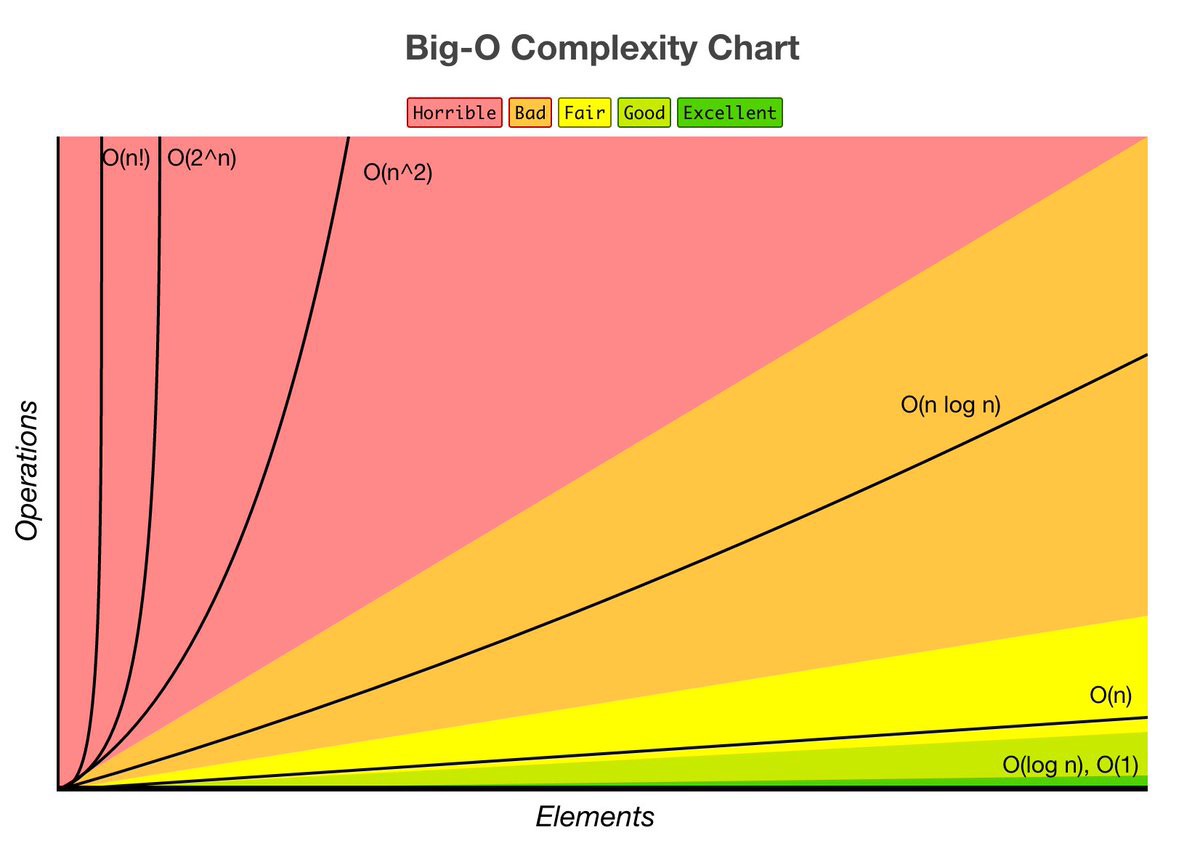
Kilka pomocnych komentarzy do obrazku:
- Zwróć uwagę na zieloną strefę, gdzie występuje zarówno złożoność stała, jak i logarytmiczna. Jak widać na powyższym przykładzie liczb, złożoność logarytmiczna jest bardzo wydajna. Jest prawie tak samo dobra, jak stała.
- Złożoność O(n * log n) – najlepsza złożoność sortowań uniwersalnych. Jeszcze do tego wrócimy.
- Mimo, że złożoność kwadratowa znajduje się w czerwonej strefie („okropnej”) warto przypomnieć sobie, że zadania są różne. A czasami jest wymagana podwójna weryfikacja. To akurat będzie miejsce, gdzie powinieneś zaglądać, kiedy będziesz chciał zoptymalizować obszary logiki celem zwiększenia wydajności. O metodach i podejściach porozmawiamy nieco dalej.
- Bardzo ważnym momentem jest początek wszystkich wykresów. Widać, że wszystkie wykresy startują z tego samego punktu i nawet w przypadku małych wartości ich wzrost nie jest jeszcze tak zauważalny i krytyczny. Dlatego właśnie trzeba testować swoje algorytmy na jednym użytkowniku / towarze / zapisie, a w warunkach rzeczywistych (najlepiej z zapasem). Inaczej zarówno w przypadku O(1), jak i O(n^2), i nawet О(n!) będą jednakowe wyniki (jedynka do kwadratu – jedynka, silnia z jedynki – jedynka).
Struktury danych
Zanim przejdziemy do przykładów z życia wziętych, musimy poradzić sobie z dwoma najpopularniejszymi strukturami danych, które pozwalają nam zastosować różne skuteczne optymalizacje (a następnie będą również bardziej złożone, ale jednocześnie bardzo ciekawe struktury danych).
Przede wszystkim wyjaśnijmy, czym są struktury danych. Tak jak poprzednio, określimy to jednym zdaniem: jest to pewien sposób na uporządkowanie danych umożliwiający ich efektywne wykorzystanie. Nic skomplikowanego ... Posiadamy dane, którymi cały czas zarządzamy, i chcemy w jakiś sposób je uporządkować, żeby następnie efektywnie je wykorzystywać (zarządzać).
Co najczęściej robimy z danymi? Wszystkie zadania sprowadzają się przeważnie do poniższych operacji:
- dostęp (uzyskać dane);
- wyszukiwanie (znaleźć dane);
- wprowadzanie (dodać dane);
- kasowanie (usunąć dane).
Po to właśnie mamy mnóstwo różnych struktur, niektóre są w czymś lepsze, a niektóre są gorsze pod kątem wydajności w porównaniu z innymi. Obraz niżej unaocznia niektóre struktury danych oraz jakiej złożoności wymaga każda z czterech operacji.
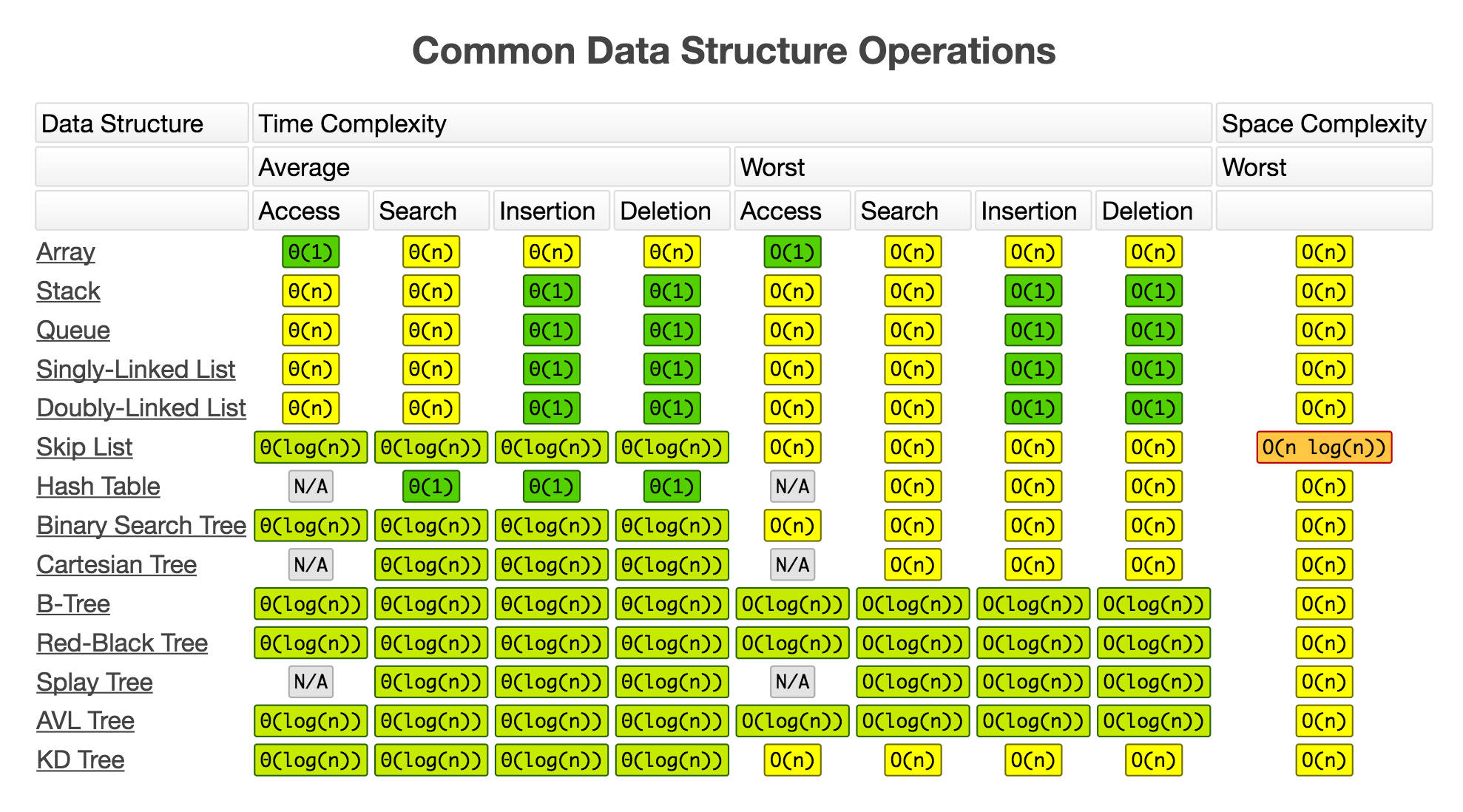
Developer powinien zdawać sobie sprawę, że występują różne struktury o różnej wydajności służące do wykonania różnych zadań. I znajomość struktur danych oznacza po prostu efektywne korzystanie z najbardziej odpowiadającej (najbardziej wydajnej) struktury do rozwiązywania jakiegokolwiek zadania. Często wyszukujesz? Wybierasz to. Masz dużo do wprowadzania? Wybierasz coś innego. Masz dużo do przenoszenia i kasowania? Wybierasz coś jeszcze innego.
Następnie porozmawiajmy o najbardziej charakterystycznych przykładach i o właściwym stosowaniu.
Tablice
Pierwszą i być może najpopularniejszą strukturą są tablice. Spójrzmy na to, co najczęściej robimy z tablicami i przeanalizujemy złożoność. Tu mamy tablicę:
const arr = [1, 2, 3];
Co możemy z nią zrobić? Najwidoczniej odwołać się do któregoś z elementów poprzez odpowiedni indeks.
arr[1]; // 2
Jak uważacie, jaka będzie złożoność tej operacji? Ten, kto przypuścił (lub wiedział), że to O(1), miał rację. Możemy natychmiast poprzez unikatowy identyfikator (indeks) uzyskać dowolny element tablicy (nawet którego tam nie ma, po prostu uzyskamy undefined). Tak samo można zapisywać poprzez indeks.
arr[0] = 4; // [4, 2, 3]
Ale lepiej tego nie robić (zazwyczaj) w ten sposób, ponieważ może to skutkować powstaniem „dziurek” w tablicy i innymi skutkami mutacji. Ale to już inny temat.
Dobra, porozmawiajmy o metodach: na przykład dodawanie elementu na końcu tablicy.
arr.push(4); // [1, 2, 3, 4]
Złożoność takiej operacji będzie O(1).
Uwaga. Dodawanie elementu na koniec listy w JavaScript jest operacją stałą, ale nie zwykłą, tylko „zamortyzowaną”. Co to znaczy? W JS nie zarządzamy pamięcią bezpośrednio, ale w językach programowania, kiedy nią zarządzamy, tworzenie tablic na nasze potrzeby będzie różnić się. To się wiąże z koniecznością przydzielenia pamięci na tablicę o odpowiednim rozmiarze. Czyli przydzielając pamięć na tablicę zawierającą 20 elementów i mając zamiar dodać 21-szy, będziemy zmuszeni przydzielić więcej pamięci, co jest operacją О(n). Mimo że nie robimy tego w JavaScript, to się dzieje w „zapleczu technicznym”. Wprawdzie będziemy głównie wstawiać elementy w O(1), czasami mogą wystąpić „skoki”, gdy dla naszego nowego elementu zostanie przydzielona większa ilość pamięci. Tak więc ta operacja jest jakby stała, ale zamortyzowana.
Jak wygląda sytuacja z usuwaniem z końca tablicy?
arr.pop(); // [1, 2, 3]
Tu też mamy O(1). No dobrze, a jak wygląda sytuacja z zadaniami polegającymi na dodawaniu i usuwaniu elementów z początku tablicy?
arr.shift(); // [2, 3]
arr.unshift(4); // [4, 2, 3]Jak wiele osób wie (lub domyśla), tu mamy inną sytuację. Dodawanie i usuwanie elementów z początku listy ma złożoność О(n). A wszystko dlatego, że zarządzając elementami na początku listy, powinniśmy aktualizować indeksy wszystkich kolejnych elementów. Jeśli doszło do usunięcia, to element, który był drugi, powinien stać się pierwszym, drugi trzecim, itd. To samo dzieje się, gdy dodajemy na początku: należy zaktualizować indeksy wszystkich kolejnych elementów.
To są znacznie mniej skuteczne rozwiązania. Zresztą sam to widzisz. To dlatego różne operacje na stosach (stack) są oparte na push & pop, a nie na unshift & shift. Kilka słów o stosach. Wyobraź sobie, że leży przed tobą stos dokumentów do podpisu: dokument, który leży na górze stosu, weźmiemy do podpisu jako pierwszy. Jeżeli coś dodajemy, dokładamy na wierzch i ten dokument będzie podpisany jako pierwszy. To jeszcze się nazywa LIFO – ang. Last In, First Out (w dosłownym tłumaczeniu oznacza: ostatnie przyszło, pierwsze wyszło). Poniżej podajemy kilka najbardziej popularnych zastosowań stosu w programowaniu: cofanie zmian w edytorach kodów lub wstecz/dalej w przeglądarkach internetowych.
Na koniec warto wspomnieć o innych metodach tablic, które mają złożoność О(n) (jak w przykładzie indexOf). Będą to prawie wszystkie metody tablicowe, czyli zawsze, kiedy coś filtrujemy, wyszukujemy, sortujemy, odwracamy i nawet zamieniamy na łańcuch (toString), to wszystko ma złożoność O(n).
Obiekty
Drugą strukturą pod względem popularności są obiekty. Służą do wygodnego przechowywania z możliwością szybkiego zarządzania danymi. Zanim przejdziemy do przykładów, rzućmy okiem na operacje. Nie jest ich dużo, pomogą ci lepiej zrozumieć poniższe idee i ich zalety.
const obj = {
id: 1,
name: 'Adam',
};Tak wygląda standardowy obiekt. Możemy określić każdą z jego właściwości wg „nazwy właściwości”, która jest identyfikatorem unikatowym. Będzie to natychmiastowa operacja niezależnie od metody.
obj.id // 1
obj['name'] // ‘Adam’Tak samo możemy nadpisać właściwości lub nawet zapisać nowe, to wszystko będzie operacją stałą.
obj.surname = 'Leos';
obj['name'] = [];Możemy również poprosić o wszystkie klucze albo wszystkie wartości obiektu. Służą temu specjalne metody, zwracające nam tablicę wartości.
Object.keys(obj) // ['id', 'name']
Object.values(obj) // [1, 'Adam']
Jak można się domyślić, złożoność tych metod to О(n): trzeba przejrzeć wszystkie wartości, tworząc z nich tablicę.
Właśnie przez to, że każda właściwość obiektu jest identyfikatorem unikatowym i dzięki temu możemy natychmiast uzyskiwać, zapisywać i aktualizować dane, obiekty są często wykorzystywane jako struktura wspomagająca różne optymalizacje poprzez mapowanie. Dla wielu osób ta definicja może być znana patrząc na odpowiedniki w innych językach: słownik (dictionary) lub mapa (map). Swoją drogą do ES2015 w JS też został dodany obiekt Map, przeznaczony do takiego właśnie stosowania. Jak ktoś nie wie, on zapewnia metody dla wszystkich czynności wykonanych wcześniej na obiekcie, imitując Map. Na przykład:
- zweryfikować, czy jest zapis (has), zamiast porównania z undefined.
- uzyskać z użyciem kluczy (get) i zapisać (set).
- zastosować forEach od razu do map, iterując na miejscu (klucz, znaczenie).
- pozostałe wygody.
Przyjrzyjmy się teraz stosowaniu. Zacznijmy od rozwiązania bardzo popularnego zadania na rozmowach kwalifikacyjnych (np. miałem ustnie rozwiązać takie zadanie na rozmowie kwalifikacyjnej w Microsoft). Zadanie – obliczyć liczbę unikatowych znaków w łańcuchu. Rozwiązanie jest banalne i to się sprawdza w przypadku wszystkich znaków:
function countSymbols(string) {
// nasza struktura wspomagająca – mapa unikatowych znaków
const map = new Map();
// uruchamiamy weryfikację
for (let i = 0; i < string.length; i++) {
const char = string[i]; // bierzemy każdy znak iteracyjny
let newValue = 1; // i ile razy go spotkaliśmy, domyślnie jeden
// jeżeli już spotkaliśmy znak, czyli znak został zapisany w karcie, powiększamy
if (map.has(char)) newValue += map.get(char)
// aktualizujemy tyle razy, ile razy spotkaliśmy znak
map.set(char, newValue);
}
return map;
}Wynikiem będzie mapa, zawierająca unikatowe znaki ich liczbę:
Map(3) { a → 2, d → 1, m → 1 } // 'adam'
Map(4) { m → 1, i → 4, s → 4, p → 2 } // 'mississippi'
Map(10) { "Х" → 1, "а" → 1, 0 → 3, "с" → 1, " " → 1, "р" → 1, "@" → 1, "з" → 1, "н" → 1, "г" → 1 } // 'chaos różnych rzeczy'Czyli stworzyliśmy mapę i dodaliśmy znaki z łańcucha, gdzie każdy znak jest unikatowym identyfikatorem. W ten sposób mogliśmy natychmiast sprawdzić, czy on widnieje się na mapie, uzyskać wartość i nadpisać ją. I to się sprawdzało w przypadku każdego znaku każdego języka, znaków specjalnych i nawet spacji. W każdym razie, zrozumiałeś o co chodzi z mapowaniem: stworzenie struktury wspomagającej do poszczególnych operacji О(1). Omówmy teraz ich zastosowanie praktyczne.
Praktyczne mapowanie
Tutaj chciałbym podać jeden przykład, ponieważ zastosowałem to w jednej z poprzednich firm. Dlaczego akurat ten przykład? Pokazuje bowiem naocznie sytuację, kiedy brak znajomości algorytmów i ich złożoności doprowadza do ogromnego spadku wydajności, przy czym na pierwszy rzut oka kod jest dobry. Tu wyraźnie widać, w jaki sposób można osiągnąć duży wzrost wydajności (prawie 100-krotny wzrost) przy odrobinie wysiłku (w pół godziny).
Krótki opis projektu: kiedyś tworzyłem aplikację do transmitowania video w czasie rzeczywistym na ReactJS + Node.js do platform alternatywnych typu Smart TV i konsoli gier wideo.
Był jeden problem, który został rozwiązany jeszcze zanim dołączyłem do projektu. Sytuacja była następująca. Nasza aplikacja zawiera tysiące programów: jakieś seriale, filmy – cały wideo content aplikacji o następującej strukturze (wszystko jest uproszczone i ma zmienioną nazwę, aby ułatwić zrozumienie i spełnić wymagania zdefiniowane w NDA, wszelkie podobieństwo do zdarzeń i osób jest przypadkowe):
const shows = [
{
id: 1,
name: 'Rick and Morty',
categories: [
'Comedy',
'Animated',
'Science',
],
data: 1001010101001011,
},
{/.../},
{/.../},
{/.../},
{/.../},
];Czyli tablice zawierające mnóstwo obiektów, reprezentujących poszczególne programy i przechowujące informacje dot. tego programu – standardowe ID, nazwę i inne.
W pewnym momencie otrzymujemy kolejną tablicę zawierające „zbanowane” programy. Z pewnych powodów nie chcemy pokazywać użytkownikowi tego programu: jakiś problem z użytkownikiem, lub kanał podjął decyzję, że tego nie będzie dziś pokazywał, albo w ogóle wystąpił problem z emisją akurat na tym kanale akurat dla tego użytkownika i pozostałe budzące wątpliwości przyczyny biznesowe. Mamy tablicę zawierającą inne obiekty, przechowujące odrobinę informacji, wystarczającej do zbanowania niektórych programów „na miejscu”.
const bannedShows = [
{
id: 1,
categories: [
'Comedy',
'Animated',
'Science',
],
},
{/.../},
{/.../},
{/.../},
];I tu podaję kod, w jaki sposób to zostało rozwiązane:
function ineffectiveBanning(shows) {
// zaczyna się weryfikacja wszystkich programów
shows.forEach(show => {
// bierzemy ID każdego programu
const { id: showID } = show;
// uruchamia się weryfikacja zbanowanych programów
bannedShows.forEach(bannedShow => {
// bierzemy teraz ID każdego zbanowanego programu
const { id: bannedShowID } = bannedShow;
// porównujemy ID i w przypadku zbieżności — oznaczamy program jako zbanowany
if (showID === bannedShowID) {
show.isBanned = true;
}
});
});
};
Co tu się dzieje? Zaczyna się cykl wszystkich programów, bierzemy ID każdego programu i uruchamiamy weryfikację zbanowanych programów, by znaleźć zbieżności. Jeżeli znaleźliśmy zbieżności, program ma być zbanowany (zaznaczamy flagą isBanned).
Problem już zdążył być zauważony przez czujne oko (i ewentualnie, ten ktoś ma tiki nerwowe). Generalnie wykonuje się tutaj zbyt dużo niepotrzebnych operacji: dla każdego programu uruchamiamy iterację zbanowanych programów, co skutkuje bardzo dużym i niepotrzebnym obciążeniem. A przecież bardzo łatwo to zoptymalizować, potrzebujemy tylko mapy zbanowanych ID, za pomocą której moglibyśmy natychmiast sprawdzić, czy program jest zbanowany, czy nie. Można to zrealizować zarówno za pomocą zwykłych obiektów, jak i za pomocą Map czy nawet Set (Set to tylko zestaw, czyli działamy jak w przypadku Map, ale nie przypisujemy żadnych wartości, jedynie dodajemy unikatowe klucze, żeby znalazły się w zestawie, i natychmiast weryfikujemy, czy widnieją się):
function effectiveBanning(shows) {
const bannedShowsIDs = new Set();
// uzupełniliśmy Set zbanowanym ID
bannedShows.forEach(({ id }) => bannedShowsIDs.add(id);
shows.forEach(({ id }) => {
// jeżeli ID bieżącego programu widnieje się w zestawie zbanowanych – zaznaczamy go
if (bannedShowsIDs.has(id)) show.isBanned = true;
});
};Co się zmieniło: wyszczególniliśmy zagnieżdżoną pętlę iterowania dot. zbanowanych programów i weryfikujemy ją tylko raz w celu uzupełnienia naszego Set, który będzie zestawem wszystkich zbanowanych ID, będziemy mogli natychmiast weryfikować, czy widnieje się tam określony zapis. W końcu nie uruchamiamy wielu niepotrzebnych pętli wewnątrz weryfikacji wszystkich programów, a jedynie natychmiast weryfikujemy pod kątem występowania iterowanego programu na liście (Set) zbanowanych. I jeżeli mamy zbieżność, zaznaczamy program jako zbanowany.
Jest zarówno krótszy sposób realizacji, jak i bardziej rozszerzony i dostępny. Można zastosować obiekt zamiast Set i po prostu dodać zapis w obiekcie, gdzie kluczem będzie ten sam unikatowy ID zbanowanego programu, a znaczeniem – cokolwiek, ewentualnie typ boolowski true. I następnie, aby zweryfikować, czy został zbanowany iterowany program, wystarczy po raz kolejny zweryfikować obiekt po ID, i dostaniemy albo true, co oznacza, że program ma być zbanowany, albo undefined, co oznacza, że program nie znalazł wśród zbanowanych, zatem pomijamy.
Świetnie. Kwestia optymalizacji została mniej-więcej wyjaśniona (rób mniej operacji, opieraj się na złożoności i wyjdzie Ci to na dobre). A o co chodzi z pamięcią?
Pamięć – praktyczne zastosowanie
Jeśli chodzi o pamięć, tu też wszystko jest proste (choć mniej przejrzyste). Jako następnym przykładem posłużę się optymalizacją, która już została przeze mnie wdrożona w trakcie realizacji bieżącego projektu w PlutoTV (również aplikacja do transmitowania video w czasie rzeczywistym na React pod telewizory i konsole gier wideo).
Był taki piękny i funkcyjny kod:
function enhanceApiResponse(apiResponse) {
const channels = apiResponse.channels
.filter(filterEmptyTimelines)
.map(addIdentificator)
.map(modifyImages)
.map(removeParams)
.map(setSession)
// more code
}Tutaj otrzymaliśmy jakąś odpowiedź zawierającą kanały i inne oraz jakoś dostosowaliśmy do swoich potrzeb: wyfiltrowaliśmy, coś dodaliśmy, coś usunęliśmy, coś przestawiliśmy. Zostało to wykonane w sposób właściwy stosując osobne metody w zależności od operacji.
Czy ktoś już zauważył, jaki powstał problem dot. pamięci? Do czego służą metody filter i map? Zwracają nową tablicę, wymagającą przydzielenia pamięci, ewentualnie dużego obszaru pamięci (ewentualnie nadspodziewanie dużego obszaru w przypadku niektórych platform). Podczas gdy ta tablica jest jedynie po to, by uruchomić za jej pomocą nowy cykl i wykonać inną operację o takich samych elementach, jak w poprzednim cyklu. Zwyczajne marnotrawstwo pamięci zupełnie bez powodu!
To wszystko można naprawić w sposób bardzo prosty, zastępując wszystko jedną weryfikacją. Np. za pomocą reduce:
function enhanceApiResponse(apiResponse) {
const channels = apiResponse.channels.reduce((acc, channel) => {
if (!hasEmptyTimelines(channel.timelines)) {
acc.push(
setChannelURL(reduceImagesObject(addIDToChannel(channel)));
);
}
return acc;
}, []);
// more code
}
Jak widzimy, idea jest bardzo prosta. Mamy jeden reduce. Oczywiście sposób zapisywania może być zarówno krótszy, jak i bardziej rozszerzony, co kto lubi. Chodzi o to, że nie przydzielamy dużego obszaru pamięci na nowe tablice, których tak naprawdę nie używamy. Taka mała optymalizacja pozwoliła nam zaoszczędzi sporo miejsca w pamięci aplikacji (od 10% do 30%) w zależności od wieku urządzenia. To jest bardzo dużo: 30% dla jednego obszaru podczas, gdy cała aplikacja potrzebuje przestrzeni, zapewniającej sprawne działanie.
Sortowania
Warto ogarnąć jeszcze sortowania. Od razu powiem, że konieczność realizacji jakiegoś unikatowego sortowania będzie powstawała bardzo rzadko (albo nie zdarzy się w ogóle w całej zawodowej karierze), ponieważ w każdym języku programowania stosowane są dobrze zoptymalizowane metody sortowań (świetny przykładem będą optymalizacji array.sort() w JavaScript, które przeanalizujemy dalej). Ale sortowania niezależnie od konieczności ich realizacji służą świetnym przykładem algorytmów i równowagi między czasem i wykorzystaniem pamięci. Przyjrzyjmy się więc bliżej dwom najpopularniejszym sortowaniom o bardzo różnym zużyciu zasobów.
W pierwszej kolejności skupmy się na najbardziej znanym algorytmie sortowania — sortowanie bąbelkowe (Bubble Sort). Polega na sprawdzaniu całej tablicy, wyszukiwaniu największego elementu i przesunięciu go na koniec tablicy. Najwidoczniej, żeby posortować w taki sposób, że za jednym razem przesuwamy tylko jeden największy element, zatem będzie trzeba przejść cały ciąg n razy (gdzie n – wielkość tablicy). Natomiast kiedy trzeba będzie przejść cały ciąg n razy i każdy będzie wymagał pełnej weryfikacji, złożoność wynosi O(n^2). Zresztą sam wiesz.
Spójrzmy na wizualizację, a następnie skupmy się na realizacji.
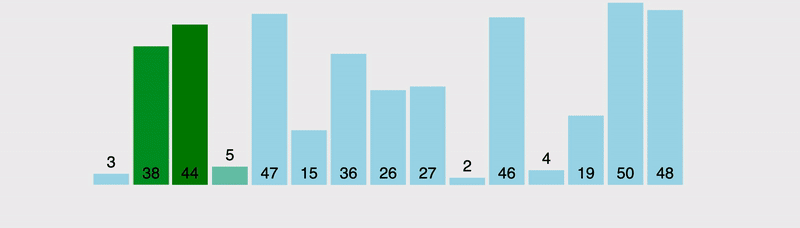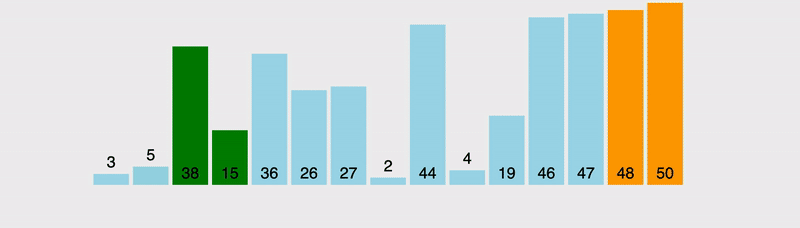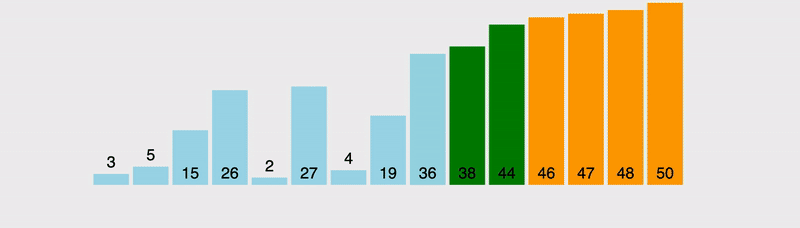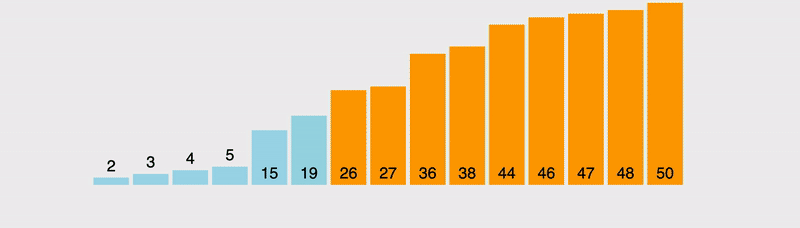
Jak widać, procedura sortująca, która używa sortowania bąbelkowego jest bardzo prymitywna: sprawdzenie całej tablicy, porównywanie dwóch kolejnych elementów. Jeżeli lewy jest większy od prawego, zamieniamy miejscami i przechodzimy do kolejnego. Tak więc każdy element jest tak długo przesuwany w ciągu, aż napotkany zostanie element większy od niego, wtedy w następnych krokach przesuwany jest ten większy element.
Kod też będzie bardzo prosty.
function bubble(arr) {
const length = arr.length;
for (let i = 0; i < length; i++) {
for (let j = 0; j < length — i — 1; j++) {
const current = arr[j]; // element bieżący
const next = arr[j + 1]; // kolejny
// jeżeli bieżący jest większy od kolejnego to zamieniamy je miejscami
if (current > next) {
arr[j] = next;
arr[j + 1] = current;
}
}
}
return arr;
}Czy powyższe sortowanie, mające kwadratową klasę złożoności obliczeniowej, nie nadaje się do stosowania z powodu tego, że występują bardziej uniwersalne sortowania? Wcale nie. Jak mogłeś zauważyć, sortowanie bąbelkowe (podobnie jak sortowanie przez wstawianie) ma jedną bardzo ważną zaletę – zużycie pamięci. Tu będzie nam potrzebna tylko jedna zmienna pomocnicza do zamiany miejscami dwóch elementów, czyli stała złożoność. Powyższe bardzo się różni od kolejnego szybkiego uniwersalnego sortowania – sortowanie przez scalanie. Przyjrzyjmy się z bliska temu pojęciu.
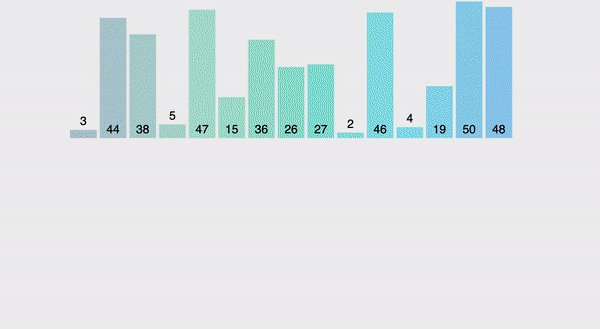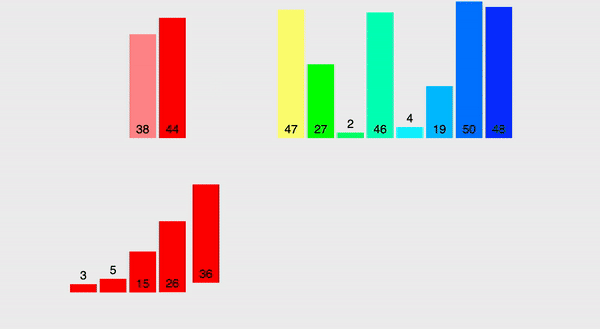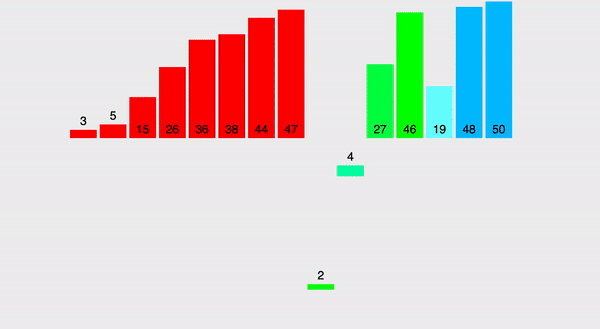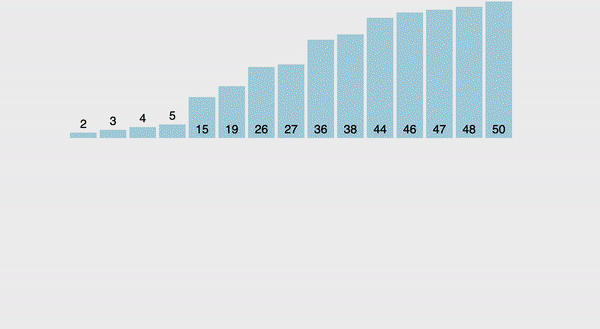
Za pierwszym razem ciężko zrozumieć, o co chodzi, ale za chwilę wszystko ogarniemy. Ideą sortowania jest dzielenie zbioru na dwie części, następnie każdą z nich także dzielimy na dwie części, czynność powtarzamy do momentu otrzymania podtablic jednoelementowych. Następnie scalamy z powrotem w jedną tablicę łącząc elementy w pary, dokładnie tak jak dzieliliśmy. W ten sposób możemy bardzo szybko wypełniać tablicę oraz sortować ją na miejscu, po prostu podejmując decyzję, który element na poszczególnym etapie należy wstawić (czyli wstawiamy cały czas mniejszy element i uzyskujemy zbiór posortowany rosnąco).
Dzięki temu, że cały czas dzielimy na pół i scalamy łącząc elementy w pary złożoność tego sortowania wynosi O(n * log n), czyli wielkość zbioru (trzeba co najmniej raz zweryfikować tablicę), mnożona przez logarytm (złożoność wynikająca ze stałego dzielenia na pół). Teraz spójrzmy na kod i na jeszcze jedną wizualizację, i wszystko będzie jasne.
Oto główny kod, który jednocześnie będzie stosowany rekurencyjnie i będzie służył do dzielenia zbioru na pół i sortowania tych dwóch połów. (Samą metodę sortowania omówimy w szczegółach trochę później).
function mergeSort(unsortedArray) {
// warunek wyjścia z rekursji
// jeżeli przekazana tablica zawiera mniej niż dwa element – sortowanie nie jest wymagane
if (unsortedArray.length < 2) {
return unsortedArray;
}
// znajdujemy środek poprzez operację bitową przesunięcia o jeden bit w prawo
// operacja ta jest równoważna dzieleniu przez 2 i zaokrąglenia w dół, tylko bardziej skutecznie i elegancko
const middle = unsortedArray.length >> 1;
const left = unsortedArray.slice(0, middle); // lewa część
const right = unsortedArray.slice(middle); // prawa część
// cała magia sortowania polega na tej metodzie merge
return merge(
mergeSort(left), mergeSort(right)
);
}Spójrzmy na inną wizualizację, która wyraźnie pokazuje, jak zbiory dzielą się i scalają się z powrotem. Od razu po wizualizacji przejdziemy do metody merge.

Na czym będzie polegała idea scalania? U nas występują dwie tablice: lewa i prawa. I jedna i druga już zostały posortowane (patrz wyżej) lub po prostu składają się z jednego elementu. Teraz musimy zweryfikować i jedną, i drugą (wystarczy jedna weryfikacja ustawiając dwa wskaźnika: pierwszy wskazuje na iterowany element lewego zbioru, drugi – na iterowany element prawego zbioru) i wybieramy mniejszy z dwóch elementów, wrzucając go do nowego zbioru, który zwrócimy jak posortowany.
function merge(left, right) {
const resultArray = []; // posortowany zbiór, który uzupełnimy i zwrócimy
let leftIndex = 0; // wskaźnik weryfikacji lewego zbioru
let rightIndex = 0; // wskaźnik weryfikacji prawego zbioru
// sprawdzamy, dopóki przynajmniej jedna z tablic nie zostanie skończona
// (to znaczy, że w drugiej tablicy pozostałe elementy są zdecydowanie)
while (leftIndex < left.length && rightIndex < right.length) {
// jeżeli lewy element jest mniejszy od prawego
if (left[leftIndex] < right[rightIndex]) {
resultArray.push(left[leftIndex]); // dodajemy go do tablicy
leftIndex++; // inkrementujemy wskaźnik, żeby powoływać się na kolejny element
} else { // inaczej prawy element jest większy, robimy to samo, tylko z prawym
resultArray.push(right[rightIndex]);
rightIndex++;
}
}
// zwracamy tablicę, która została uzupełniona i dodajemy wszystko, co nie zostało zweryfikowane
return resultArray
.concat(left.slice(leftIndex))
.concat(right.slice(rightIndex));
}Myślę, że tutaj wszystko już jest jasne. Jeszcze tylko dodam, że wystarczy, że zweryfikujemy co najmniej jedną tablicę do końca, ponieważ pozostałe niesprawdzone liczby zdecydowanie będą większe, po prostu trzeba je dodać na końcu naszego posortowanego zbioru. (Wstawiamy to na koniec kodu, czyli tam gdzie wrzucamy pozostałe elementy metodą concat.)
Teraz sam się przekonałeś, że szybsze sortowanie wymaga więcej dostępnej pamięci (na te wszystkie nowe zbiory przydzielane są duże obszary pamięci, ale to nic w porównaniu z zużyciem stałym w przypadku sortowania bąbelkowego).
Tak więc już mamy wiedzę na temat tego, jakiego rodzaju optymalizacje są ukryte w „zapleczu technicznym” array.sort(). Mimo że implementacje mogą różnić się w zależności od przeglądarki (i nawet w zależności od wersji), globalna idea polega na tym, żeby posługiwać się sortowaniem przez scalanie i sortowaniem szybkim (także O(n * log n)) w zależności od rodzaju danych w tablicy. Ale tablice nie dzielą się na podtablice do jednego elementu, jak w naszej implementacji. Zamiast tego zbiór osiągnie swój koniec po uzyskaniu 10 elementów, i już wobec tych zbiorów składających się z 10 elementów stosuje się sortowanie przez wstawianie (odpowiednik sortowania bąbelkowego, O(n^2)). I dopiero po tym uruchamiamy algorytm sortowania przez scalanie / sortowania szybkiego. W ten sposób możemy zaoszczędzić bardzo dużo pamięci (nie tworzymy zbędnych tablic), szybkość działania pozostaje praktycznie na tym samym poziomie (sortowanie przez wstawianie jest dość skuteczne w przypadku małych tablic). Oto wspaniały przykład równowagi między szybkością działania i wykorzystaniem pamięci.
Ważne podsumowanie sortowań: nie bez powodu kilkukrotnie pisałem o tym, że sortowanie przez scalanie i sortowanie szybkie to są najlepsze sortowania uniwersalne. Oznacza to, że charakteryzują się stabilnością i świetnie się sprawdzą w każdej sytuacji i w przypadku każdego rodzaju danych (oczywiście w granicach zdrowego rozsądku). Chociaż tak, są różne sortowania o złożoności lepszej od O(n * log n): np. radix sort. Ale mają wąski (nieuniwersalny) zakres stosowania. Chociaż takie sortowania oczywiście mają szeroki zakres stosowania, po prostu są skuteczne w konkretnych sytuacjach.
Wnioski
- Nie musisz znać się na wszystkich algorytmach i strukturach danych. Przyswajanie wiedzy podstawowej, z której czerpią najwięcej korzyści, przychodzi szybko i z łatwością.
- Nie wszystkie implementacje warte są zapamiętywania, możesz nawet zapomnieć o niektórych najważniejszym. Wystarczy jeden raz pochylić się nad nimi, żeby mieć pojęcie o możliwościach.
- Analizuj swoje algorytmy. Zastanów się nad ich wydajnością. Od wydajności stworzonego kodu zależy wydajność i niezawodność stworzonego przez Ciebie produktu (oraz Twoje umiejętności developerskie).
Przydatne materiały
Teoria:
- The complexity of simple algorithms and data structures in JS;
- Introduction to Data Structures and Algorithms.
Praktyka:

